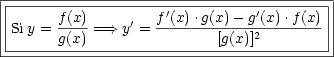Temario

MODULO 1. Introducción al cálculo en dos variables.

1.1 Funciones en dos variables. 
1.2 Derivadas parciales. 
1.3 Máximos y mínimos de funciones de dos variables. 
1.4 Aplicaciones: Optimización de funciones de dos variables que representen       gastos, ingresos o utilidad.

   

MODULO 2. Integración

2.1 Antiderivada. 
2.2 Integral indefinida. 
2.2.1 Integración con condiciones iniciales. 
2.3 Fórmulas básicas de integración. 
2.3.1 Integral indefinida de una constante. 
2.3.2 Integral de una constante por una variable. 
2.3.3 Integral de xn 
2.3.4 Integral de en 
2.3.5 Integral de una constante por una función de x. 
2.3.6 Integral de una suma (diferencia) de funciones. 
2.3.7 Regla de la potencia. 
2.3.7.1 Integrales que incluyen un 
2.3.7.2 Integrales que incluyen funciones exponenciales. 
2.3.8 Integrales que incluyen funciones logarítmicas. 
2.3.9 Integrales que incluyen (1/u)du 
2.3.10 Integrales incluyen au             2.3.11 Integral por partes. 
2.4 Aplicaciones: Determinación de funciones de costo, utilidades, consumo, y ahorro a partir de sus marginales.

MODULO 3. Integral Definida

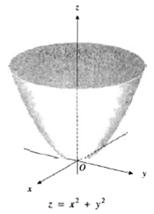
3.1 Área bajo la curva. 
3.2 Teorema Fundamental del cálculo. 
3.3 Propiedades de la integral definida. 
3.4 Área entre una y dos curvas. 
3.5 Aplicaciones: Excedente del consumidor y del productor, valor presente y valor futuro.

MODULO 4. Sistemas de ecuaciones lineales y matrices

4.1 Sistemas de ecuaciones lineales. 
4.1.1 Definición 
4.1.2 Sistemas de ecuaciones lineales: consistentes, inconsistentes, y su representación paramétrica del conjunto solución. 
4.1.3 Métodos para resolución de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución, eliminación (sumas y restas). 
4.1.4 Sistemas de ecuaciones equivalentes. 
4.1.5 Eliminación de Gauss y Gauss-Jordan. 
4.1.5.1 Definición de matriz. 
4.1.5.2 Expresión matricial de un sistema de ecuaciones lineales. 
4.1.5.3 Operaciones elementales sobre renglones. 
4.1.5.4 Reducción de Gauss y Gauss-Jordan. 
4.1.5.5 Sistemas homogéneos. 
4.2 Álgebra de Matrices 
4.2.1 Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta). 
4.2.2 Operaciones con matrices (suma, diferencia, multiplicación por escalar y producto de matrices). 
4.2.3 Propiedades de las operaciones con matrices. 
4.2.4 Matriz inversa. 
4.3 Determinantes 
4.3.1 Definición de un determinante. 
4.3.2 Expansión por cofactores. 
4.3.3 Propiedades de los determinantes. 
4.3.4 Regla de Cramer. 

4.4 Aplicaciones: Modelo insumo-producto, análisis de ventas y comportamiento del consumidor. 

MODULO 1. Introducción al cálculo en dos variables.

Objetivo Particular del Periodo:

El alumno comprenderá los conceptos básicos del cálculo diferencial en varias variables, así como la resolución de problemas en el entorno económico-administrativo, enfatizando aquellos del área de optimización de recursos. 

1.1 Funciones en dos variables.

Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.

El conjunto de parejas ordenadas para las cuales la regla de correspondencia dá un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contradominio.

Una función de dos variables se denota usualmente con la notación

z = f (x, y)

Las variables x, y se llaman variables independientes, y z se llama variable dependiente.

La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).

Este conjunto de puntos forma una superficie en el espacio tridimensional.

En consecuencia, la gráfica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,y puede intersectar a la gráfica de f en mas de un punto.

La función f del ejemplo 1 es el conjunto de todos los pares ordenados de la forma (P, z) tales que

 z=v25- x2 -y2

Por tanto, la grafica de f es la semiesfera en el plano x y por arriba de este cuyo centro es el origen y tiene radio 5. Esta semiesfera se muestra en la figura 1.

Ejemplo 2: dibuje la gráfica de la función

Sol/: la gráfica de f es la superficie que tiene la ecuación z=x2 +y2 . La traza de la superficie en el plano x,y se obtiene al utilizar la ecuación z=0 simultáneamente con la ecuación de la superficie. Al hacerlo resulta x2 +y2=0 la cual representa el origen. Las trazas en los planos xz y yz se obtiene al emplear las ecuaciones z=x2 +y2. Estos trazos son las parábolas z= x2 y z= y2.

 http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml#ixzz3rhfv8i3v



Ficha bibliográfica: 

Marlon Fajardo Molinares. (2009). Funciones de dos y más variables, dominio y rango, y curva de nivel.. 21 Nov. 2015, de Monografias.com S.A Sitio web: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml#ixzz3rhfv8i3v

Ficha bibliográfica: 

Academatica. (2013). Video de funciones de dos variables - introducción. 21 Nov. 2015, de Academatica Sitio web: https://www.youtube.com/watch?v=9FpkWkqCDV0


1.2 Derivadas parciales.

Se llama derivada parcial de una función con respecto a la variable independiente al siguiente límite, si existe y es finito:






calculado suponiendo y constante.

Se llama derivada parcial de una función con respecto a la variable independiente al siguiente límite, si existe y es finito:




calculado suponiendo x constante.

Para calcular las derivadas parciales son válidas las reglas y fórmulas de derivación ordinarias. Basta considerar que todas las variables son constantes (son números), salvo aquella respecto de la que estamos derivando.


http://www.matap.uma.es/~svera/probres/pr3/pr3_1.html#derivadas


Ficha bibliográfica: 
Salvador Vera . (2000). Cálculo para la Ingeniería. 21 de noviembre de 2015, de satd Sitio web: http://www.matap.uma.es/~svera/probres/pr3/pr3_1.html#derivadas

 Ficha bibliográfica: 

Academatica. (2010). Derivadas Parciales . 21 Nov. 2015, de Academatica Sitio web: https://www.youtube.com/watch?v=bKGCity6dr8

1.3 Máximos y mínimos de funciones de dos variables.


Definición. Una función   tiene un máximo (mínimo) en un punto  si el valor de la función en este punto es mayor (menor) que su valor en cualquier otro punto X(x,y) de algún entono de P.

Condiciones necesarias de extremo. Si una función diferenciable  alcanza un extremo en el punto  entonces sus derivadas parciales de primer orden en este punto son iguales a cero, o sea:

;

Los puntos en los que las derivadas parciales son iguales a cero se llaman puntos críticos o estacionarios. No todo punto crítico es un punto extremo.

Condiciones suficientes para la existencia de extremos.

(a) Caso de dos variables. Sea  un punto crítico de una función   con las derivadas parciales de segundo orden continuas en P, y sea  el determinante de su matriz hessiana, entonces:


Es decir, si el hessiano es positivo hay extremo (el tipo nos lo da  , si es negativa máximo y si es positiva mínimo). Si el hessiano es negativo no hay extremo. Y si el hessiano es cero hay duda (que habrá que resolver por otro método)

http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html

 Ficha bibliográfica: 

Salvador Vera. (2000). Cálculo para la Ingeniería. 21 Nov. 2015, de satd Sitio web: http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html

Ficha bibliográfica: 

Academatica. (2013). Máximos y mínimos funciones de dos variables. 21 Nov. 2015, de Academatica Sitio web: https://www.youtube.com/watch?v=dhhmhSAOEug

1.4 Aplicaciones: Optimización de funciones de dos variables que representen gastos, ingresos o utilidad.

El punto de equilibrio sirve para determinar el volumen mínimo de ventas que la empresa debe realizar para no perder, ni ganar.

En el punto de equilibrio de un negocio las ventas son iguales a los costos y los gastos, al aumentar el nivel de ventas se obtiene utilidad, y al bajar se produce pérdida.

Se deben clasificar los costos:

Costos fijos: Son los que causan en forma invariable con cualquier nivel de ventas.
Costos variables: Son los que se realizan proporcionalmente con el nivel de ventas de una empresa.


Ventas en punto de equilibrio = Costos Fijos x  
1
1 – Costos variables
Ventas
Ejemplo: En el año 200x, la empresa XYZ tuvo ingresos por concepto de ventas de $6.750.000, en el mismo periodo sus costos fijos fueron de $2.130.000 y los costos variables de $3.420.000

Ventas en punto de equilibrio = $2.130.000 x  
1
1 – $3.420.000
$6.750.000
Ventas en punto de equilibrio  =  $4.346.938

El nivel de ventas para no ganar, ni perder es de $4.346.938, este es el punto de equilibrio para la empresa.

El costo fijo permanece invariable, independientemente del volumen de ventas, mientras que el costo variable está relacionado directamente con el volumen de ingresos o ventas.


El porcentaje del costo variable en el punto de equilibrio está dado por la relación existente entre los costos variables y el nivel de ventas, así:


Porcentaje de costo variable = Costo Variable x 100
Ventas
Porcentaje de costo variable = $3.420.000 x 100
$6.750.000
Los costos variables en el punto de equilibrio son $4.346.938  X  51%  =  $2.216.938

Comprobación del punto de equilibrio

Ventas 4.346.938
 (-) Costos variables 2.216.938
 = Utilidad Bruta en Ventas 2.130.000
 (-) Costos fijos 2.130.000
 = Utilidad neta 0
Aplicación del punto de equilibrio

En la práctica, el punto de equilibrio sirve para calcular el volumen de las ventas que debe realizar una empresa para obtener un porcentaje de utilidad determinado. La fórmula es la siguiente:

Ventas = Ventas en punto de equilibrio + Porcentaje de Utilidad deseado + % de Costo variable

Ejemplo: La XYZ empresa desea obtener una utilidad del 20% sobre el punto de equilibrio. Determinar el volumen de ventas necesario para obtener dicha utilidad. (Utilizando los datos de los ejemplos anteriores).


Ventas = Ventas en punto de equilibrio + Porcentaje de Utilidad deseado + % de Costo variable

Ventas = 4.346.938 + 20%(4.346.938) + 51%(4.346.938)

Ventas = 4.346.938 + 869.387 + 2.216.938

Ventas = 7.433.263

Aplicación

Ventas 7.433.263
 (-) Costos variables 3.790.964
 = Utilidad Bruta en Ventas 3.642.299
 (-) Costos fijos 2.130.000

 = Utilidad neta 1.512.299

http://www.gestiopolis.com/como-calcular-el-punto-de-equilibrio/

 Ficha bibliográfica: 

Gómez Giovanny. (2001). Cómo calcular el punto de equilibrio. 21 Nov. 2015, de gestiopolis Sitio web: http://www.gestiopolis.com/como-calcular-el-punto-de-equilibrio/

Resumen:
En este modulo volvimos a recordar el tema de las funciones, y nos introducimos a las derivadas y sus diferentes tipos y aplicaciones a la hora de representar gastos, ingresos y utilidades.

MODULO 2. Integración

Objetivo Particular del Periodo:

El alumno entenderá el concepto de integral y su relación con la derivada. Resolverá problemas de aplicación dando énfasis a aquellos relacionados con las áreas económico-administrativas tales como: Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.

2.1 Antiderivada.

Concepto:
Dada una función, sabemos como hallar su derivada, este problema
lo estudia el cálculo diferencial. Cuando se conoce la derivada de
una función y se desea conocer la función original, se usa el cálculo

integral. 

La antiderivada o primitiva de una función f(x) es otra función F(x)+C

donde C es una constante. Si al derivar F(x)+C nos da como respuesta f(x)

Es decir F’(x) = f(x)

A la función F(x) se le llama una antiderivada de la una función f(x). 

Ejemplo ¿Qué se derivo para que la derivada sea xf = 4?

Por el método de Ensayo y Error se puede ver que la funcion que se

derivo es:

F1 (x)= 4x pero también las funciones

F2 (x)=4x+5

F3 (x)=4x-2

F4 (x)=4x-12

F5 (x)=4x+15

F6 (x)=4x+8

F(x) = 4x+C

Es decir que la funcion cuya derivada es 4 es una familia de

funciones en este caso lineales cuyos miembros todos tienen

pendiente de +4 pero diferentes intersecciones con el eje y como

vemos en las graficas para los diferentes valores de la constante C

C =0 C=5 C=-2 C=12 C=15 C=8 

 Ficha bibliográfica: 

ANTONIO NARIÑO . (2012). ANTIDERIVADAS. 21 Nov. 2015, de solucionesdeingenio Sitio web: http://sosa.solucionesdeingenio.com/wp-content/uploads/2012/09/antiderivada.pdf

 Ficha bibliográfica: 

wilmer Duran. (2011). ANTIDERIVADAS.calculo WILEDU. 21 Nov. 2015, de wilmer Duran Sitio web: https://www.youtube.com/watch?v=1ftsUqvnn8Q


2.2 Integral indefinida.

Cuando estudiamos el problema del área y el problema de la distancia analizamos que tanto el valor del área debajo de la gráfica de una función como la distancia recorrida por un objeto se puede calcular aproximadamente por medio de sumas o bien exactamente como el límite de una suma.

[f(x₀) + f(x₁) + f(x₂) + ……………………… + f(x_n–1)] D x = 

 [f(x₁) + f(x₂) + f(x₃) + ……………………… + f(x_n)] D x =

(se utiliza el valor de la función en el extremo derecho de cada subintervalo)

 [f(t₁) + f(t₂) + f(t₃) + ……………………… + f(t_n)] D x = 

(se utiliza el valor de la función en cualquier punto de cada subintervalo

Este tipo de límites aparece en una gran variedad de situaciones incluso cuando f no es necesariamente una función positiva. Teniendo en cuenta lo expresado surge la necesidad de dar un nombre y una notación a este tipo de límites.

Definición 1: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica a es el número

= [f(x₀) + f(x₁) + f(x₂) + ……………………… + f(x_n–1)] D x o bien

=  donde x₀ = a, x_n = b y D x = .

(la función se evalúa en el extremo izquierdo de cada subintervalo [x_i-1, x_i] con i = 1, .., n)

Definición 2: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica es el número:

=[f(x₁) + f(x₂) + f(x₃) + ……………………… + f(x_n)] D x

= donde x₀ = a, x_n = b y D x = .

(la función se evalúa en el extremo derecho de cada subintervalo [x_i-1, x_i] con i = 1, .., n)

Definición 3: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica es el número:

= [f(t₁) + f(t₂) + f(t₃) + ……………………… + f(t_n)] D x

= donde x₀ = a, x_n = b y D x = .

(la función se evalúa en cualquier punto t_i de cada subintervalo [x_i-1, x_i] con i = 1, .., n)

El número a es el límite inferior de integración y el número b es el límite superior de integración .

Notación y terminología:

http://www.fca.unl.edu.ar/Intdef/IntegralDefinida.htm

 Ficha bibliográfica : 

Purcell, E. y Varberg, D.. (1993). Cálculo Diferencial e Integral. 21 Nov. 2015, de Prentice Hall Hispanoamericana Sitio web: http://www.fca.unl.edu.ar/Intdef/IntegralDefinida.htm

2.2.1 Integración con condiciones iniciales.



Hemos estado analizando temas de gran importancia que son necesarios para entender el entorno que rodea al cálculo de integrales. Así que para continuar con el mismo camino, en esta ocasión tocaremos un tema que también es muy interesante y ayudara a comprender mejor el mundo de las integrales. Me refiero a la constante de integración.


Dentro del cálculo, cualquier integral indefinida de una función se escribe siempre con una constante, la cual se llama constante de integración. La constante de integración se encarga de expresar una ambigüedad inherente a la construcción de primitivas.

Como ya lo sabes, al derivar cualquier función constante, obtendremos como resultado cero. Una vez encontrado dicho resultado se considera una primitiva F a la cual se le puede sumar o restar una constante C, con lo cual se obtiene otra primitiva. Con esto lo que se trata de explicar es que la constante es una manera de expresar que cualquier función cuenta con un número infinito de primitivas diferentes.

Para un mejor entendimiento te invito a que observes las funciones que se te presentan a continuación, en las que podemos darnos cuenta de que la constante C puede tomar valores diferentes tal y como se te explico anteriormente, valores que pueden ser restados o sumados a la función original. Los ejemplos son los siguientes:

f(x) = x + 2
f(x) = x – 8
f(x) = x + 1
Podemos observar que en estos ejemplos, las constantes de integración tienen valores de 2, -8 y 1. Ahora supongamos que derivamos las 3 funciones, y obtenemos los siguientes resultados:

f ‘ (x) = x
f ‘ (x) = x
f ‘ (x) = x

Como te puedes dar cuenta, los resultados de las 3 funciones son el mismo, ¿A qué se debe esto?, ¿Qué pasó con los valores 2, -8 y 1? Es importante aclarar que dentro del cálculo diferencial estos valores tienen un valor de 0, al contrario del cálculo integral, donde son de gran importancia si se quieren obtener las funciones originales a partir de las funciones que ya han sido derivadas.

Ficha bibliográfica: 

Yibram Eduardo Jaimes Basa . (2012). La constante de integración y sus condiciones iniciales. 21 Nov. 2015, de calculointegralunivia Sitio web: https://calculointegralunivia.wordpress.com/2012/03/23/la-constante-de-integracion-y-sus-condiciones-iniciales/

 Ficha bibliográfica: 

Exito en matematicas. (2014). Ecuacion diferencial con condiciones iniciales. 21 Nov.2015, de Exito en matematicas Sitio web: https://www.youtube.com/watch?v=oKTBAgkrR9U

2.3 Fórmulas básicas de integración. 

Recordemos que como en las derivadas, las integrales poseen reglas, propiedades y formulas para su procedimiento. Las integrales poseen un signo en su inicio en forma de S alargada y con una terminación de dx, esto las diferencia de otras ecuaciones. Una integral a realizar siempre ira acompañada de una S alargada al inicio y un dx al final. Estas son las formulas básicas de integración.

La integral de “n” numero siempre será nx + C. Ejemplo

La integral de una constante siempre será constante * variable +C (ax+C)

La integral de X elevado a “n” numero será ^Xn+1, lo que se haga en la exponenciación de la X se pondrá también abajo dividiéndola, es una regla establecida. Ejemplo

La integral que divide arriba sobre una variable abajo será logaritmo natural de variable mas C. La formula marca lnX+C porque arriba en dx no tiene constante ni variable pero sí un 1 imaginario, ejemplo.

La integral de un producto se puede separar siempre y cuando no se altere su ecuación. De esta forma se integra en partes. No tienen que ser 3 productos necesariamente para usar la formula ;)  Ejemplo.

La integral de un Binomio (V) es parecida a la formula 3, solo que acá al sacar la derivada del binomio (dv) se comprueba que exista la derivada fuera de V, en caso que no exista, se iguala hasta quedar exacto y se elimina, quedando solo el binomio (V) mas la exponenciación + 1.

Se saca el binomio que es (2+X²)
La derivada del binomio es 2X y se le agrega dx, queda 2Xdx. Se comprueba que 2X coincida con el producto de afuera que es X, como es 2X y tenemos X solamente, entonces se tiene que igualar a 2X…¿Cómo?, multiplicando  2(X), lo que hagamos dentro se hace afuera pero en reciproco. Y se elimina la igualdad quedando lo restante.

Ya que se elimino el producto de afuera, se procede con la formula 3, y el ½ estará multiplicando al resultado que quede de la formula.

El 2 que esta en la división del binomio tiene que desaparecer, no se puede multiplicar directo con el 2 de afuera. Para eliminarlo se debe multiplicar medios con medios, extremos con extremos.

https://ingenieriaensistemasuat.wordpress.com/2010/12/14/381/

 Ficha bibliográfica: 

locoraphael. (2010). Introducción a las Formulas básicas de Integración.. 22 Nov. 2015, de ingenieriaensistemasuat Sitio web: https://ingenieriaensistemasuat.wordpress.com/2010/12/14/381/

2.3.1 Integral indefinida de una constante. 

La integral de una constante es igual a la constante por x.

Ejemplo

Integral de cero

ficha bibliográfica es : 

inetor. (2015). integral de una constante . 22 Nov. 2015, de inetor Sitio web: http://www.inetor.com/indefinidas/integral_constante.html

ficha bibliográfica es : inetor. (2015). integral de una constante . 22 Nov. 2015, de inetor Sitio web: http://www.inetor.com/indefinidas/integral_constante.html

 Ficha bibliográfica: 

Tareasplus. (2011). Integral de una constante. 22 Nov. 2015, de Tareasplus Sitio web: https://www.youtube.com/watch?v=GR6Tin6Epzg

2.3.2 Integral de una constante por una variable. 

 El cálculo de la integral indefinida es muy parecido al de la integral definida con la diferencia que al final no necesitamos poner los valores ni del límite superior de la integración ni del límite inferior de la integración.
Esto también significa que la solución de la integración indefinida nunca es un número, sino una función del integrando dado. La forma más fundamental para computar la integración de un integrando dado es,

Para integrar un integrando de la forma exponencial, donde el exponente es alguna variable, solo incremente el valor del exponente de la variable por uno y coloque el nuevo exponente en el denominador de la variable dada. Está bastante claro que el valor de n = −1 no es admisible dado que este convertiría el valor del denominador en cero, resultando este en un valor indefinido como respuesta.

Otro método básico de la integración es,

Esto significa que la integración de una constante producirá la variable de integración como salida con la constante dada como su coeficiente.

Existen algunas fórmulas de integración las cuales se utilizan directamente para la integración de funciones trigonométricas, funciones exponenciales, funciones logarítmicas, etc.


 Ficha bibliográfica: 

Lauro Soto. (Definicion De Integral Indefinida). Definicion De Integral Indefinida. 22 Nov. 2015, de mitecnologico Sitio web: http://mitecnologico.com/igestion/Main/DefinicionDeIntegralIndefinida

http://mitecnologico.com/igestion/Main/DefinicionDeIntegralIndefinida

 Ficha bibliográfica: 

Janet Lopez. (2012). Derivada de una constante por una variable. 22 Nov. 2015, de Janet Lopez Sitio web: https://www.youtube.com/watch?v=l6IRgULsAdM

2.3.3 Integral de xn 

Potencia de x.

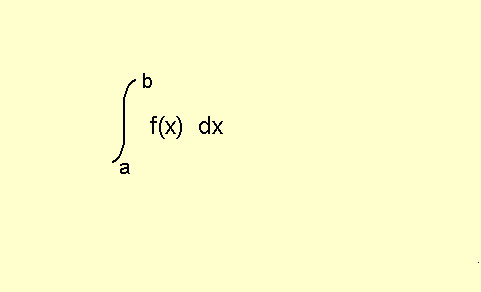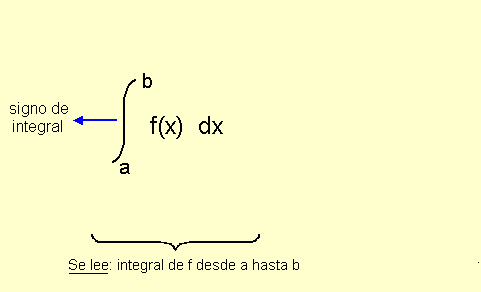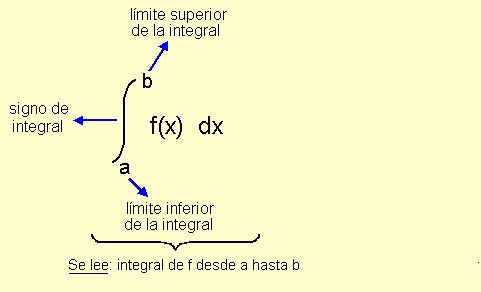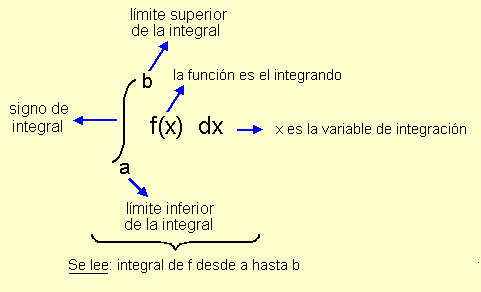
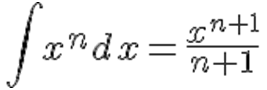
xn dx = x(n+1) / (n+1) + C (n 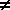 -1)

1/x dx dx = ln|x| + C

Exponente / Logaritmo

ex dx = ex + C	bx dx = bx / ln(b) + C
ln(x) dx = x ln(x) - x + C

Trigonométrica

sen x dx = -cos x + C	cos x dx = sen x + C	tan x dx = -ln|cos x| + C
csc x dx = - ln|csc x + cot x| + C	sec x dx = ln|sec x + tan x| + C	cot x dx = ln|sen x| + C

Resuelta Trigonométrica

cos x dx = sen x + C	sen x dx = -cos x + C	sec2 x dx = tan x + C
csc x cot x dx = -csc x + C	sec x tan x dx = sec x + C	csc2 x dx = -cot x + C

Trigonométrica Inversa

arcsen x dx = 1  (1-x2) + C	arccsc x dx = -1 |x|(x2-1) + C
arccos x dx = -1  (1-x2) + C	arcsec x dx = 1  |x|(x2-1) + C
arctan x dx = 1 1+x2 + C	arccot x dx = -1 1+x2 + C

Hyperbólica

senh x dx = cosh x + C	cosh x dx = senh x + C	tanh x dx = ln( cosh x ) + C
csch x dx = ln( tanh(x/2) ) + C	sech x dx = atan( senh x ) + C	coth(x) dx = ln( senh x ) + C

Presione la Demostración para ver una demostración/discusión del teorema.

http://math2.org/math/integrals/es-tableof.htm

Ficha bibliográfica: 
David Manura. (1995-2003). Tablas Matemáticas de David: Tabla de Integrales. 22 Nov. 2015, de math2.org Sitio web: http://math2.org/math/integrals/es-tableof.htm


2.3.4 Integral de en 



Ejemplo principal Una bomba está entregando agua a un tanque a una razón de

r(t) = 3t2 + 5 litros/minuto
donde t es el tiempo en minutos desde el momento que la bomba es encendido. ¿Quánto agua es bombeado en el tanque durante los primeros dos minutos?
Primero estimación: r(t) es el número de litros de agua por minuto bombeado en el tanque. En el momento que es encendido la bomba, esta razón es

r(0) = 3(0)2 + 5 = 5 litros/minuto,
así que el volumen total de agua bombeado en el tanque durante los primeros dos minutos debe ser aproximadamente:
Volumen total bombeado = Número de litros/minuto × Número de minutos
≈ r(0) × 2
= 5 × 2 = 10 litros.
Aquí está una gráfica que muestra la curva y la calculación acabamos de hacer



Toma en cuenta dos hechos:
La cantidad estimada de agua bombeada en el tanque es igual a la área del rectángulo rojo.
Hemos signíficamente subestimado el volumen de agua bombeado en el tanque porque, como muestra la gráfica, la razón a la que está entrando agua sube a medida que pasa el tiempo; por ejemplo, la razón es de
r(1) = 3(1)2 + 5 = 8 litros/minuto
Sin embargo, usamos en cambio la razón inicial, r(0) = 5 litros/minuto, como la razón durante el periodo entero [0, 2].
Por lo tanto, vamos a estimar de nuevo la cantidad de agua a través de una calculación minuto-por-minuto, usando la razón de cambio al inicio de cada minuto para la duración de aquel minuto:

Minuto 1: Volumen total bombeado = Número de litros/minuto al inicio de minuto 1 × Número de minutos
≈ r(0) × 1
= 5 × 1 = 5 litros
Minuto 2: Volumen total bombeado = Número de litros/minuto al inicio de minuto 2 × Número de minutos

Ficha bibliográfica: 

Stefan Waner. (2012). la integral. 22 Nov. 2015, de zweigmedia Sitio web: http://www.zweigmedia.com/MundoReal/tutorials4/framesIntegralGraphical.html

2.3.5 Integral de una constante por una función de x. 


Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).

Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:

F'(x) = f(x).

Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.

[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.

Se representa por ∫ f(x) dx.

Se lee : integral de f de x diferencial de x.

∫ es el signo de integración.

f(x) es el integrando o función a integrar.

dx es diferencial de x, e indica cuál es la variable de la función que se integra.

C es la constante de integración y puede tomar cualquier valor numérico real.

Si F(x) es una primitiva de f(x) se tiene que:

∫ f(x) dx = F(x) + C

Para comprobar que la primitiva de una función es correcta basta con derivar.


Propiedades de la integral indefinida

1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.

∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx

2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

∫ k f(x) dx = k ∫f(x) dx

http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

 Ficha bibliográfica: 
math2me. (2012). Integral de una constante. 22 Nov. 2015, de math2me Sitio web: https://www.youtube.com/watch?v=Mmy6zolldfw

2.3.6 Integral de una suma (diferencia) de funciones. 

(a) Reglas de sumas y diferencias

[f(x) ± g(x)] dx

=

f(x) dx

±

g(x) dx

 Reglas de sumas y diferencias


En palabras:

La integral de la suma de dos funciones es la suma de las integrales de las funciones individuales, y la integral de la diferencia de dos funciones es la diferencia de las integrales de las funciones individuales.

(b) Regla de múltiples constantes

kf(x) dx

=

k

f(x) dx

(k constant)

En palabras:

Para tomar la integral de una constante multiplicada por una función, se toma la integral de la función sola, y después se multiplica la respuesta por la constante. (En otras palabras el constante "sigue para el paseo" )
¿Por qué son válidas estas reglas? Porque la derivada de una sum es la suma de las derivadas, y el caso es parecido para diferencias y múltiplos constantes.


http://webcache.googleusercontent.com/search?q=cache:V0Wah9Wwys0J:www.zweigmedia.com/MundoReal/Calcsumm6.html+&cd=1&hl=es&ct=clnk&gl=mx&client=firefox-a

Ficha bibliográfica: 
Stefan Waner. (2007). La integral. 22 de Nov. 2015, de zweigmedia Sitio web: http://webcache.googleusercontent.com/search?q=cache:V0Wah9Wwys0J:www.zweigmedia.com/MundoReal/Calcsumm6.html+&cd=1&hl=es&ct=clnk&gl=mx&client=firefox-a

 Ficha bibliográfica: 

math2me. (2012). Integral de la suma o resta de funciones. 22 Nov. 2015, de math2me Sitio web: https://www.youtube.com/watch?v=yn_hFO6W6Jk

2.3.7 Regla de la potencia.


Regla de Potencias
La derivada de una potencia o función potencial, es igual al exponente por la base elevada al exponente menos uno y por la derivada de la base.






Con base a la regla de potencias te presentamos un video explicativo sobre el tema y algunos ejemplos que te pueden ayudar para el desarrollo de tu aprendizaje:

http://derivadasencalculo.blogspot.mx/p/regla-de-potencias.html

 Ficha bibliográfica: 
Derivadas en Calculo. (2011). Regla de Potencias. 22 Nov. 2015, de Derivadas en Calculo Sitio web: https://www.youtube.com/watch?v=kKAwT1dzI30





2.3.7.1 Integrales que incluyen un 

 Ficha bibliográfica: 
lasmatesyyo. (2013). Derivada de u a la n. 22 de Nov. 2015, de lasmatesyyo Sitio web: https://www.youtube.com/watch?v=DKdOtd72vW8


2.3.7.2 Integrales que incluyen funciones exponenciales. 


Método y ejemplos de como encontrar la integral indefinida de la función exponencial cuando se encuentra multiplicada por la derivada del exponente
Dicha integral es igual a la función exponencial dividida por el logaritmo natural de la base de dicha función exponencial
En el vídeo se muestran ejemplos de distinta índole de complejidad ya que no siempre es posible vislumbrar que nos encontramos frente a este tipo de integral (denominada por algunos como una integral inmediata)

A lo largo de nuestra serie de vídeos de cálculo integral hemos venido hablando de diversas técnicas para hallar la primitiva de una función. Básicamente se han explorado dos fórmulas potentes que nos servían para encontrar la integral de una función a la n por su derivada, y cuando queremos encontrar la integral de l derivada sobre la función. Estas tienen unos casos particulares, y vimos mediante cambio de variable cómo podemos simplificar algunas funciones para llevarlas a los casos anteriormente mencionados. De ahora en adelante vamos a llamar estos tipos de integrales como integrales de tipo potencial o integrales de tipo logarítmica, respectivamente. Este par de integrales se denominan comúnmente como integrales inmediatas, ya que nacen en realidad de las derivadas. 

En este vídeo vamos a hablar de un nuevo tipo de integral conocido como exponencial, y se deduce entonces de la fórmula de la derivada de un “a” a la f(x), una fórmula nueva para encontrar primitivas. Podemos decir entonces que cuando tengamos que encontrar la integral de una función exponencial por la derivada de su exponente, vamos a decir que es igual a tener la exponencial dividida por el logaritmo natural de la base de dicha función. El ejemplo más simple y útil de recordar, es la de la integral de e a la x, que es igual a tener e a la x más c. De allí podemos deducir entonces que cuando tengamos que hallar la integral de e a la f(x), es igual a tener e a la f(x)+C. En el video se desarrollan algunos ejemplos para mostrar cómo hallar entonces este tipo de integrales de manera rápida, identificando quien es f(x) y f’(x). No en todos los casos vamos a encontrarnos con la derivada tal cual, sino algo similar, y mediante una serie de “artilugios” podemos llegar a la integral, incluso utilizando la sustitución.


https://aula.tareasplus.com/Roberto-Cuartas/CALCULO-INTEGRAL/Integral-de-la-funcion-exponencial


 Ficha bibliográfica: 

Roberto Cuartas . (2014). Integral de la función exponencial. 22 de Nov. 2015, de tareasplus Sitio web: https://aula.tareasplus.com/Roberto-Cuartas/CALCULO-INTEGRAL/Integral-de-la-funcion-exponencial

 Ficha bibliográfica: 

Tareasplus. (2012). Integral de la función exponencial. 22 de Nov. 2015, de Tareasplus Sitio web: https://www.youtube.com/watch?v=NXtNSiUXSfI

2.3.8 Integrales que incluyen funciones logarítmicas. 

Integrales logaritmicas

Integrales exponenciales

http://www.vitutor.com/integrales/indefinidas/integrales_logaritmicas.html

 Ficha bibliográfica: math2me. (2012). Funciones con logaritmo natural (integral por sustitución). 22 de Nov. 2015, de math2me Sitio web: https://www.youtube.com/watch?v=3m-10Npe_IQ



2.3.9 Integrales que incluyen (1/u)du 

.Ficha bibliográfica: 

lasmatesyyo. (2013). Integrales de la forma du/u. 22 de Nov. 2015, de lasmatesyyo Sitio web: https://www.youtube.com/watch?v=9xS3kKGU2-A




2.3.10 Integrales incluyen au 
          





ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon.

 2.3.11 Integral por partes. 
Integración por partes es un análogo de la regla del producto para derivadas, aunque su fórmula es un pocito más complicada. Aunque, cuando haces integración por partes a través del método tabular mostramos aquí no necesitarás ningunas fórmulas, y el método es tan simple que, al terminar este tutorial, te preguntarás por qué todos los demás tienen ¡tantos problemas con este tema!
P Por lo que he escuchado, el método tabular solo se aplica a tipos específicos de problemas integración por partes. ¿És verdad? 

R No es verdad. El método tabular como lo presentamos aquí se aplica a cada tipo de problema integración por partes, y por lo tanto nunca tendrás que saber el método tradicional anticuado hacerlo que da tanta dificultad a tus amigos.
Primero, un poco de notación: Si u es una función, denotar si derivada por D(u) y un antiderivada por I(u). Así, por ejemplo, si u = 2x2, entonces
D(u) = 4x,      y      I(u) =  
2x3
3
 .
(Si prefiriéramos, podríamos tomar I(u) =  
2x3
3

  + 46, pero usualmente optamos par la antiderivada más simple).

Integración por partes

Si u y v son funciones continuas de x, y si u tiene una derivada continua, entonces

u ⋅ v dx  =  u ⋅ I(v) −  D(u)I(v)  dx


Ejemplos
x ⋅ e^x dx  =  x ⋅ e^x −  (1)(e^x) dx  =  xe^x − e^x + C
Forma de tabla: 
Escribe las funciones originales en el primero renglón. Luego, en el siguiente renglón, sigue las instrucciones el la parte superior de la tabla: D significa "toma la derivada" y I significa "toma la integral"

D I + x ex − 1 ex Para conseguir la formula de la tabla, sigue las flechas en cada renglón de la tabla:     (+) x ex  −  (1) ex  dv,  la misma calculación que la de la fórmula. http://www.zweigmedia.com/tuts/tutIntParts.html?lang=es  Ficha bibliográfica: Stefan Waner. (2013).Integración por partes . 22 de Nov. 2015, de zweigmedia Sitio web: http://www.zweigmedia.com/tuts/tutIntParts.html?lang=es

2.4 Aplicaciones: Determinación de funciones de costo, utilidades, consumo, y ahorro a partir de sus marginales.


DETERMINACIÓN DE FUNCIONES DE COSTO:
Servir de base para fijar precios de venta y para establecer políticas de comercialización.
Facilitar la toma de decisiones.
Permitir la valuación de inventarios.

Controlar la eficiencia de las operaciones

UTILIDADES:
Utilidad es la propiedad por la cual una cosa o acción adquiere la condición de valor útil para satisfacer las necesidades humanas. Puede hacer referencia a los siguientes términos:
 En economía: utilidad (economía) a la función de utilidad, cuya derivada es la utilidad marginal; a un criterio para encontrar el punto óptimo de eficiencia de Pareto, en el cual no es posible beneficiar a más elementos de un sistema sin perjudicar a otros; y a la subjetividad de la utilidad esperada; En filosofía: al utilitarismo, una teoría ética.
 En informática: a una herramienta que sirve de soporte para la construcción y ejecución de programas;
En el derecho registral: al catálogo de montes de utilidad pública; al monte de utilidad pública;
En contabilidad también denominado beneficio, es la diferencia entre los ingresos obtenidos por un negocio y todos los gastos incurridos en la generación de dichos ingresos; véase beneficio económico

CONSUMO Y AHORRO A PARTIR DE SUS MARGINALES.
La propensión marginal al consumo mide el incremento que se produce en el consumo cuando la renta crece en una unidad. Teniendo en cuenta que los crecimientos de la renta se destinan parcialmente a un mayor consumo y parcialmente a un mayor ahorro, la propensión marginal se sitúa entre cero y uno.
La función de consumo agregado puede escribirse de la siguiente forma:
C = a + c x Y
En esta expresión C representa el gasto de consumo, mientras que Y es la renta disponible. Cuando la renta disponible se incrementa, el gasto total de consumo crece en una proporción igual a c, que es la propensión marginal a consumir. El término a de la función de consumo se denomina consumo autónomo, y recoge aquel nivel mínimo de consumo que se realizaría aunque no se dispusiese de renta en un periodo.
Junto al concepto de propensión marginal a consumir se define el concepto de propensión media al consumo, o cociente entre el gasto total en consumo y la renta disponible. Una propiedad de esta función de consumo es que, aunque decreciente, esta propensión media es mayor que la propensión marginal:
C / Y = a/Y + c
La propensión marginal al ahorro (s) es igual a 1-c, ya que las familias destinan al ahorro (S) los incrementos de renta que no destinan al consumo.
Y = C + S
ΔY = ΔC + ΔS
1 = ΔC/ΔY + ΔS/ΔY
1 = c + s

http://www.expansion.com/diccionario-economico/propension-marginal-al-consumo-ahorro.html

 Ficha bibliográfica: 
Uxó González, Jorge. (2015). PROPENSIÓN MARGINAL AL CONSUMO/AHORRO. 29 Nov. 2015, de expansión Sitio web: http://www.expansion.com/diccionario-economico/propension-marginal-al-consumo-ahorro.html

Resumen:

En este modulo, vimos los temas de las antiderivadas, y nos introducimos también a las integrales y sus diferentes formas las cuales son: indefinida, indefinida de una constante, Integral de una constante por una variable, de la forma xn, de la forma en,Integral de una constante por una función de x,Integral de una suma (diferencia) de funciones, de la forma un,Integrales que incluyen funciones exponenciales,Integrales que incluyen funciones logarítmicas, de la forma (1/u)du, Integral por partes y la forma de aplicarlas para determinar costos.